
Back To School – Let’s calculate I3
Techniques for solving DC circuits
Referring to the following circuit, calculate direct current I3:
- Using Kirchhoff’s laws;
- Using nodal analysis;
- Applying Thévenin’s theorem at nodes A and B.
Ok, let’s dive into calculation…
Kirchhoff’s Current Law - The algebraic sum of currents at a node is zero.
Kirchhoff’s Voltage Law - The algebraic sum of voltages around a closed circuit loop is zero.
- KCL stands for Kirchhoff’s Current Law
- KVL stands for Kirchhoff’s Voltage Law
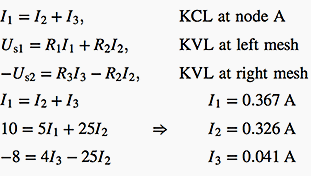
The following equation can be written:

Substituting values, we obtain:

Finally,

Thévenin’s voltage UTh at nodes A and B can be easily calculated by disconnecting the right part of the circuit:
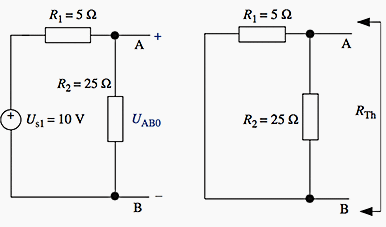
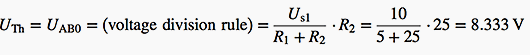
Thévenin’s equivalent resistance RTh is the resistance “seen” from nodes A and B, when all generators are deactivated (in our case, only E1 is present):
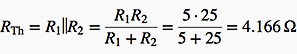
The left side of the circuit can now be substituted by its Thévenin equivalent, in order to calculate current I3:
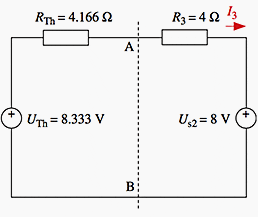
This single-mesh circuit can be easily solved using KVL (Kirchhoff’s voltage law):
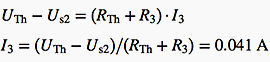
Readers should note that UAB0 ≠ UAB:
UAB = UTh – RTh · I3 = 8.333 – 4.166 · 0.041 = 8.163
Comparing the three methods, we can conclude that Thévenin’s theorem is very powerful, in particular when a single current value is needed.
Another Kirchhoff’s Laws Worked Example (VIDEO)
Cant see this video? Click here to watch it on Youtube.
Thevenin’s Theorem. Example with solution (VIDEO)
Cant see this video? Click here to watch it on Youtube.
Reference // Fundamentals of electric power engineering – Ceraolo, Massimo, Davide Poli.